Euler Function(오일러 함수)

오일러 함수 Φ(n) (Euler Φ function)

• n 보다 작고 n과 서로소인 양의 정수의 개수. Φ(1) = 1로 정의

오일러 함수에 이용되는 정리들

1. n과 m이 서로소라면 Φ(nm) = Φ(n)Φ(m)
2. p가 소수이면 Φ(p^k) = p^k–p^(k-1)
   • p^k와 서로소인 수는 p, 2p, 3p, … (p^k - 1)를 제외한 나머지 수 (p^k - p^k / p)
3. p가 소수: Φ(p) = p–1 (2번 변형)
4. Φ(2^k) = 2^(k-1) (2번 변형)

오일러 함수 정의

• 모든 수는 소수의 곱으로 나타낼 수 있으므로, 소인수분해 한 후 오일러 파이 함수가 곱셈적 함수임을 이용해서 오일러 파이 함수 계산
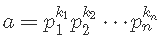  에 대하여
  
  1. 오일러 정리
• 양수 m에 대하여 gcd(a, m) = 1이면 a^Φ(m) ≡ 1 (mod m)
  • 앞에서 Ax ≡ b (mod n)를 확장된 유클리드를 이용하여 계산하였는데, a x a^(Φ(m)-1) ≡ 1 (mod m)임을 사용하여 구할 수 있다.
    1. 페르마의 소정리
  • p가 소수이면, (0 < a < p) 인 모든 a에 대해 a^(p-1) ≡ 1 (mod p)

코드

오일러 함수